LASER CAVITY DESIGN
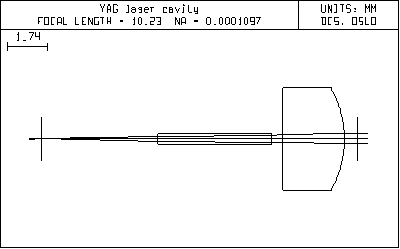
The Gaussian beam spreadsheet provides an easy way to interactively design systems that work with Gaussian beams. We will consider the design of a cavity for a hypothetical Nd:YAG laser. The task is to design a cavity to support single transverse mode oscillation in a YAG rod. The YAG rod is 0.5mm diameter and 5mm long. The cavity consists of two plane mirrors, and a focusing lens, Melles Griot part number 01LQF005. The cavity is to work in a near hemispherical geometry, as shown in the figure below. The exact length of the cavity is to be adjusted so that the spot size of the TEM 00 mode is 1/3 the diameter of the laser rod.
- To enter the system, use File >> New. Assign the file name yagcav1.len, and select catalog lens. Click 4 to dismiss the dialog box. When the Catalog database window appears, using the MG_POS catalog, enter the part number 01LQF005, then click 4 to go to the lens spreadsheet.
- The lens will originally be entered in the system backwards. To reverse it, click Row button 1 to select the element, then use the Reverse icon on the spreadsheet toolbar.
- After you have entered the lens, enter the YAG rod by inserting two surfaces in front of the lens (a quick way to do this is to click on the surface 1 row button and then press SHIFT+SPACEBAR twice). Then enter the rod data (Thickness 5.0, aperture 0.25). Set Thickness 2 to .5 and the entrance beam radius to .1. To enter the glass, first make sure that the wavelength is set to 1.064 micrometers, then click on the options button in the glass field, choose Direct from the pop-up menu, enter the name Nd-YAG, then enter the index 1.82.
- Set the object distance to 5mm, and the image distance TH[4] to 0.5mm. The object surface and image surface are to be mirrors, but it is not necessary to enter them as reflecting surfaces since they are just points in space where we want the Gaussian beam wavefront to have a certain radius of curvature. Similarly, the object numerical aperture, or equivalently the entrance beam radius, need not be set at this time, since the value will be determined using the Gaussian beam spreadsheet. When all the data has been entered, the Surface data spreadsheet should appear as follows:
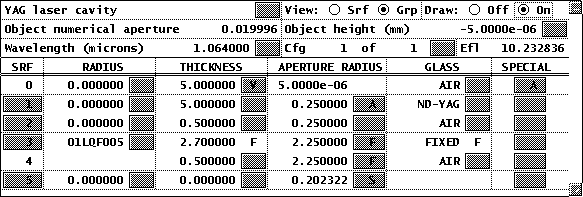
The next task is to determine the TEM 00 mode of the cavity. To do this, use Calculate >> Gaussian Beam >> Interactive ABCD Analysis. The method is to set the radius of curvature of the wavefront on the object surface to the radius of curvature of the mirror, then adjust the spot size on the object surface (the variable cell) until the radius of curvature of the wavefront on the image surface (the watch cell) is equal to the radius of curvature of the other mirror. In any stable curved mirror cavity, any wavefront can be replaced by a mirror of the same radius of curvature withoutchanging the transverse mode structure, since the wavefronts of a Gaussian beam are always spherical. If you are used to the conventions used in the laser literature, you should be especially careful about the sign conventions used in OSLO. Particularly note that OSLO takes the radius of curvature of a spherical wavefront to be positive when the center of curvature is to the right.
- After the spreadsheet is open, enter 0.0 for the radius of curvature of the wavefront on the object surface, since the mirror is plane. Enter a trial value for the spot size, 0.1. Then observe the value of the final radius of curvature in the watch cell while changing the value in the variable cell.
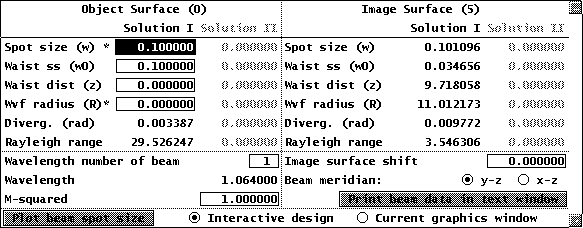
The following table shows a succession of values entered.
| Variable Cell | Watch Cell |
| .1 | 11.012173 |
| .01 | -902.043228 |
| .02 | 1.2916e04 |
| .015 | -1.2744e03 |
| .0175 | -2.2587e03 |
| .019 | -6.4480e03 |
| .0195 | -2.3166e04 |
| .0197 | 2.4960e05 |
At this point, the value is close enough to state that we have found the TEM00 mode. Next, click the Print beam data in text window button. Instead of varying the spot size, you could vary the lens data. For example, try varying the object thickness by typing th 0 5.1 in the command line. You will see that the Gaussian beam spreadsheet is updated automatically to use the new data. 
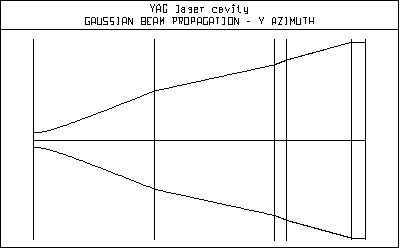
The spot size on the end of the rod is 0.1346mm, whereas the design target is 0.5/3 = 0.16667mm. The way to increase it is to move the mirrors a little farther apart (i.e. move towards the edge of the stable region). Changing the object distance to 5.1mm changes the spot size on the rod to about .205, and the spot size on the object surface to .013mm. If we set the object distance to 5.07 we find the spot size on the object surface to be .016, and the spot size on the end of the rod to be .1662, close enough for now. The final touch up could be to move the image surface mirror by the waist distance. Having determined the correct cavity spacing, we can plot the beam profile using the Plot beam spot size button in the spreadsheet. This produces an anamorphic picture of the beam, in which the z scale is the overall length of the system, and the y scale is the maximum spot size. In effect, it is a plot of true paraxial rays. On this scale, the surfaces all appear to be straight lines.
Printing the beam data to the text window produces the following data for the final system:
*GAUSSIAN BEAM – YZ PLANE WAVELENGTH = 1.064000 M-SQUARED = 1.000000
SRF SPOT SIZE DIVERGENCE WAIST SIZE WAIST DIST INC RADIUS RFR RADIUS 0 0.016000 0.021164 0.016000 1.0000e-06 5.7134e+05 5.7134e+05 1 0.016000 0.021164 0.016000 — — — 2 0.108506 0.011630 0.016000 -9.227400 -5.182691 -9.432497
3 0.166244 0.021164 0.016000 -7.817253 -14.360419 -7.890340 4 0.176782 0.014601 0.016000 -12.056947 -8.385946 -12.156528 5 0.216075 0.001567 0.216073 0.559750 -14.838308 3.3950e+04
